Definiție
Se numește matrice cu m linii și n coloane (sau de tip  ) un tablou cu m linii și n coloane:
) un tablou cu m linii și n coloane:
 ) un tablou cu m linii și n coloane:
) un tablou cu m linii și n coloane:
ale cărui elemente  sunt numere complexe.
sunt numere complexe.
 sunt numere complexe.
sunt numere complexe.
Uneori această matrice se notează și  unde
unde 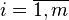 și
și  Pentru elementul
Pentru elementul  indicele i arată linia pe care se află elementul, iar al doilea indice, j, indică pe ce coloană este situat.
indicele i arată linia pe care se află elementul, iar al doilea indice, j, indică pe ce coloană este situat.
 unde
unde 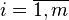 și
și  Pentru elementul
Pentru elementul  indicele i arată linia pe care se află elementul, iar al doilea indice, j, indică pe ce coloană este situat.
indicele i arată linia pe care se află elementul, iar al doilea indice, j, indică pe ce coloană este situat.
Mulțimea matricilor de tip  cu elemente numere reale se notează prin
cu elemente numere reale se notează prin 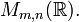 Aceleași semnificații au și mulțimile
Aceleași semnificații au și mulțimile 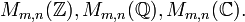
 cu elemente numere reale se notează prin
cu elemente numere reale se notează prin 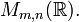 Aceleași semnificații au și mulțimile
Aceleași semnificații au și mulțimile 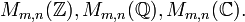
Cazuri particulare
1) O matrice de tipul  (deci cu o linie și n coloane) se numește matrice linie și are forma:
(deci cu o linie și n coloane) se numește matrice linie și are forma:
 (deci cu o linie și n coloane) se numește matrice linie și are forma:
(deci cu o linie și n coloane) se numește matrice linie și are forma:
2) O matrice de tipul 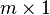 (deci cu m linii și o coloană) se numește matrice coloană și are forma:
(deci cu m linii și o coloană) se numește matrice coloană și are forma:
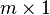 (deci cu m linii și o coloană) se numește matrice coloană și are forma:
(deci cu m linii și o coloană) se numește matrice coloană și are forma:
3) O matrice de tip  se numește nulă (zero) dacă toate elementele ei sunt zero. Se notează cu O:
se numește nulă (zero) dacă toate elementele ei sunt zero. Se notează cu O:
 se numește nulă (zero) dacă toate elementele ei sunt zero. Se notează cu O:
se numește nulă (zero) dacă toate elementele ei sunt zero. Se notează cu O:
4) Dacă numărul de linii este egal cu numărul de coloane, atunci matricea se numește pătrată:
Sistemul de elemente  reprezintă diagonala principală a matricii A, iar suma acestor elemente se numește urma matricii A notată:
reprezintă diagonala principală a matricii A, iar suma acestor elemente se numește urma matricii A notată:
 reprezintă diagonala principală a matricii A, iar suma acestor elemente se numește urma matricii A notată:
reprezintă diagonala principală a matricii A, iar suma acestor elemente se numește urma matricii A notată:
Mulțimea matricilor pătrate se notează  Printre aceste matrici, una este foarte importantă, aceasta fiind:
Printre aceste matrici, una este foarte importantă, aceasta fiind:
 Printre aceste matrici, una este foarte importantă, aceasta fiind:
Printre aceste matrici, una este foarte importantă, aceasta fiind:
și se numește matricea unitate (pe diagonala principală are toate elementele egale cu 1, iar în rest sunt egale cu 0).
Egalitatea a două matrici
Definiție. Fie  ,
,  . Se spune că matricile
. Se spune că matricile 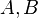 sunt egale și se scrie
sunt egale și se scrie 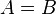 dacă
dacă 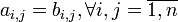
 ,
,  . Se spune că matricile
. Se spune că matricile 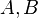 sunt egale și se scrie
sunt egale și se scrie 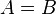 dacă
dacă 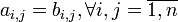
Transpusa unei matrici
Definiție. Fie  .
.
 .
.
Transpusa matricii A este:
T dată de:
dată de: 
 dată de:
dată de: 
Matrice simetrică
Definiție. Fie matricea pătrată  . Spunem că matricea
. Spunem că matricea  este simetrică dacă este egală cu transpusa ei:
este simetrică dacă este egală cu transpusa ei:  Fie M={1, 2, 3, ..., m} si N={1, 2, 3, ..., n}. A: M x N -> R, A(i,j) = ai,j se numește matrice de tipul (m, n), cu m linii și n coloane.
Fie M={1, 2, 3, ..., m} si N={1, 2, 3, ..., n}. A: M x N -> R, A(i,j) = ai,j se numește matrice de tipul (m, n), cu m linii și n coloane.
 . Spunem că matricea
. Spunem că matricea  este simetrică dacă este egală cu transpusa ei:
este simetrică dacă este egală cu transpusa ei:  Fie M={1, 2, 3, ..., m} si N={1, 2, 3, ..., n}. A: M x N -> R, A(i,j) = ai,j se numește matrice de tipul (m, n), cu m linii și n coloane.
Fie M={1, 2, 3, ..., m} si N={1, 2, 3, ..., n}. A: M x N -> R, A(i,j) = ai,j se numește matrice de tipul (m, n), cu m linii și n coloane.
O matrice care are o dimensiune egală cu 1 se numește vector. O matrice A[1,n] (1 linie și n coloane) se numește vector linie, iar o matrice B[m,1] ( o coloană și m linii) se numește vector coloană. Exemple:
Este o matrice de tipul 4x3. Elementul A[3,1] sau a3,1 este 12. este o matrice de tipul (1, 7) sau vector linie.
O matrice A(m,n) care are m = n se numește matrice pătrată. Deci, o matrice pătrată este matricea care are numărul de linii egal cu numărul de coloane.
Operații cu matrici
Adunarea matricilor
Fie 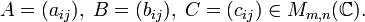
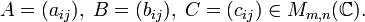
Matricea C se numește suma matricilor A, B dacă:
Observații.
1) Două matrici se pot aduna dacă sunt de același tip, adică au același număr de linii și același număr de coloane, deci 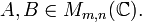
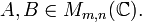
2) Explicit, adunarea matricilor A, B înseamnă:
Proprietăți ale adunării matricilor
 (Asociativitatea adunării). Adunarea matricilor este asociativă, adică:
(Asociativitatea adunării). Adunarea matricilor este asociativă, adică: (Comutativitatea adunării). Adunarea matricilor este comutativă, adică:
(Comutativitatea adunării). Adunarea matricilor este comutativă, adică: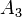 (Element neutru). Adunarea matricilor admite matricea nulă ca element neutru, adică:
(Element neutru). Adunarea matricilor admite matricea nulă ca element neutru, adică:-
 astfel încât
astfel încât 
 (Elemente opuse). Orice matrice
(Elemente opuse). Orice matrice 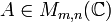 are un opus, notat
are un opus, notat 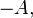 astfel încât:
astfel încât:Înmulțirea cu scalari a matricilor
Observație
A înmulți o matrice cu un scalar revine la a înmulți toate elementele matricii cu acest scalar. Deci:
Proprietăți ale înmulțirii matricilor cu scalar




Înmulțirea matricilor
Fie 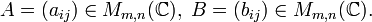
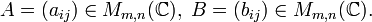
Produsul dintre matricile A și B (în această ordine), notat  este matricea
este matricea 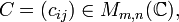 definită prin:
definită prin:
 este matricea
este matricea 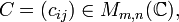 definită prin:
definită prin:
Observații
1) Produsul  a două matrici nu se poate efectua întotdeauna decât dacă
a două matrici nu se poate efectua întotdeauna decât dacă  adică numărul de coloane ale lui A este egal cu numărul de linii ale lui B, când se obține o matrice C=AB \in M_{m, p} (\mathbb C).
adică numărul de coloane ale lui A este egal cu numărul de linii ale lui B, când se obține o matrice C=AB \in M_{m, p} (\mathbb C).
 a două matrici nu se poate efectua întotdeauna decât dacă
a două matrici nu se poate efectua întotdeauna decât dacă  adică numărul de coloane ale lui A este egal cu numărul de linii ale lui B, când se obține o matrice C=AB \in M_{m, p} (\mathbb C).
adică numărul de coloane ale lui A este egal cu numărul de linii ale lui B, când se obține o matrice C=AB \in M_{m, p} (\mathbb C).
2) Dacă matricile sunt pătrate  atunci are sens întotdeauna atât
atunci are sens întotdeauna atât  cât și
cât și  iar în general,
iar în general,  adică înmulțirea matricilor nu este comutativă.
adică înmulțirea matricilor nu este comutativă.
 atunci are sens întotdeauna atât
atunci are sens întotdeauna atât  cât și
cât și  iar în general,
iar în general,  adică înmulțirea matricilor nu este comutativă.
adică înmulțirea matricilor nu este comutativă.Proprietățile înmulțirii matricilor
 (Asociativitatea înmulțirii). Înmulțirea matricilor este asociativă, adică:
(Asociativitatea înmulțirii). Înmulțirea matricilor este asociativă, adică: (Distributivitatea înmulțirii față de adunare). Înmulțirea matricilor este distributivă în raport cu adunarea matricilor, adică:
(Distributivitatea înmulțirii față de adunare). Înmulțirea matricilor este distributivă în raport cu adunarea matricilor, adică:-
 matrici pentru care au sens operațiile de adunare și înmulțire.
matrici pentru care au sens operațiile de adunare și înmulțire.
 Dacă
Dacă  este matricea unitate, atunci:
este matricea unitate, atunci:
spunem că 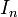 este element neutru
este element neutru
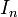 este element neutru
este element neutruDeterminanți
Articol principal: Determinant (matematică).
Dacă  este o matrice pătrată cu elemente din K, atunci numărul:
este o matrice pătrată cu elemente din K, atunci numărul:
 este o matrice pătrată cu elemente din K, atunci numărul:
este o matrice pătrată cu elemente din K, atunci numărul:
se numește determinantul lui A.


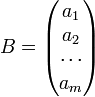




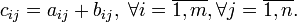





 și
și 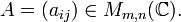 Se numește produsul dintre
Se numește produsul dintre  definită prin
definită prin 
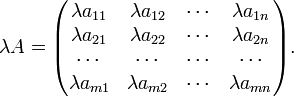



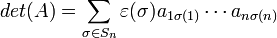
Niciun comentariu:
Trimiteți un comentariu